In our last lesson, we looked at cryptographic hash functions and attacks against them. Cryptographic hash functions are used in almost every protocol that guarantees integrity and authentication. But in a blockchain setting, one of their most important applications is in Merkle trees.

Merkle trees were invented by Ralph Merkle, one of the forefathers of modern cryptography. Though he patented the Merkle tree in 1982, the patent on them has long expired. Merkle trees are used widely in many applications, including Git, BitTorrent, ZFS, the Certificate Transparency framework, and of course, pretty much every cryptocurrency.
Let's walk through a simple example of how we might use a Merkle tree in an application.
Building up a Merkle tree
Say we're designing a file sharing protocol. We'll assume the files we're sharing are large—say, Linux distros.
In this protocol, once a user finishes downloading a file, they need to somehow verify it wasn't corrupted in transit. TCP itself can correct most random errors, but even so, corruption errors are common when dealing with files of this size. How can we ensure integrity at the application layer?
Here's an idea: let's ship a cryptographic hash alongside the Linux ISO. That way, after the user is done downloading the ISO, they can hash it and check if the digests match. Hashing is pretty fast—even on a single core you can hash hundreds of megabytes per second.

But what if the hashes don't match? How do you know where the error in the file was?
Actually, you have no way of knowing where the error was. You have to throw out all of the 2GB and restart the download, hoping this time the corruption doesn't happen. This seems like a lousy solution.
Here's an idea: what if we break up the data into blocks and ship hashes for each block?

This is nice! Now if we have a random corruption in our data, instead of downloading all 2GB over again, we can check which of the 250MB blocks came out corrupted and then only re-download that block. The downside is that we need to ship all 8 hashes alongside the download:
Block 1 digest: 743bacf85062c45f533060e3abb3dc1f02683269
Block 2 digest: 4db3539ecf02e69ffacec45751129e38bdfa469e
Block 3 digest: 0f34d88b134aece384b3d079996d08ee7eadecfd
Block 4 digest: 5bbc8a852490d2f9d9e0067f408950539af0bda9
Block 5 digest: 2ba7cb929bc68c6706b8be03946add92e941999d
Block 6 digest: ee389b56b4a6ff4407df5ffd5f675c2fa73edd22
Block 7 digest: d446b49425506732cfd707865908a99a1ab15ba7
Block 8 digest: 1f706fc900b2c4543525ea1434a201d169004a3dFor 250MB blocks this is probably fine, but if we want smaller blocks to minimize the impact of corruptions, then we need more than 8 hashes. If we wanted 128KB blocks, we'd need 15,000 hashes, and if we wanted 8KB blocks, we'd need 250,000 hashes. This becomes unwieldy pretty fast.
Here's where Merkle trees come in. Merkle trees are a kind of cryptographic accumulator. Cryptographic accumulators allow you to compact arbitrarily many pieces of data into a constant amount of space. In other words, a Merkle tree lets us represent arbitrarily many blocks while only transmitting a single hash across the wire.
Merkle trees are also known as hash trees, because they hash data upwards in a tree. It's easy to explain in code—here's how you can create a hash tree with only two elements.
from hashlib import sha1
def h(s): return sha1(s.encode()).hexdigest() # hashing helper function
block1 = "Block 1"
block2 = "Block 2"
digest1 = h(block1)
digest2 = h(block2)
root = h(digest1 + digest2)
print(root)
# d1c6d4f28135f428927a1248d71984a937ee543e
(This diagram uses the notation h(1, 2) for legibility, but it's actually h(h(1) + h(2)).)
By concatenating the two digests and taking their hash, the root of the hash tree commits to both digests. Think about it: if there were some other way to produce this same root, then that would imply the existence of a hash collision. Hash collisions should be impossible for a strong cryptographic hash function. Thus, the root of this hash tree, known as the Merkle root, must be a unique identifier of this exact tree.
(If you don't follow this argument, play around with another example in code! This intuition is really important, and we'll continue to build on it.)
The Merkle root is therefore an accumulator over all of the original data that was hashed to produce this tree. It also commits to that data in order, since we used string concatenation on the underlying blocks to combine their values. (If you had used a commutative operation like addition or XOR instead of concatenation, then technically you could've switched the order of some blocks and gotten the same root. This is undesirable, so don't make that mistake.)
How does this scale up to many blocks though? Pretty simple. We repeat this same operation across the data in layers until we get a single root.
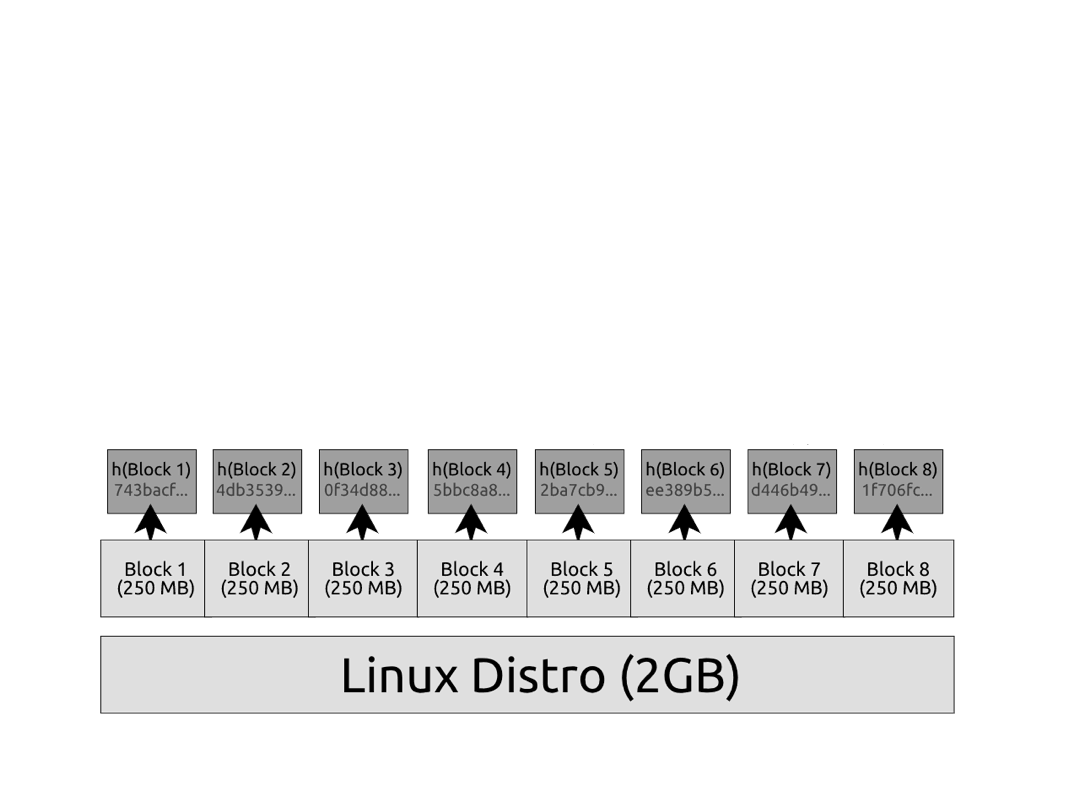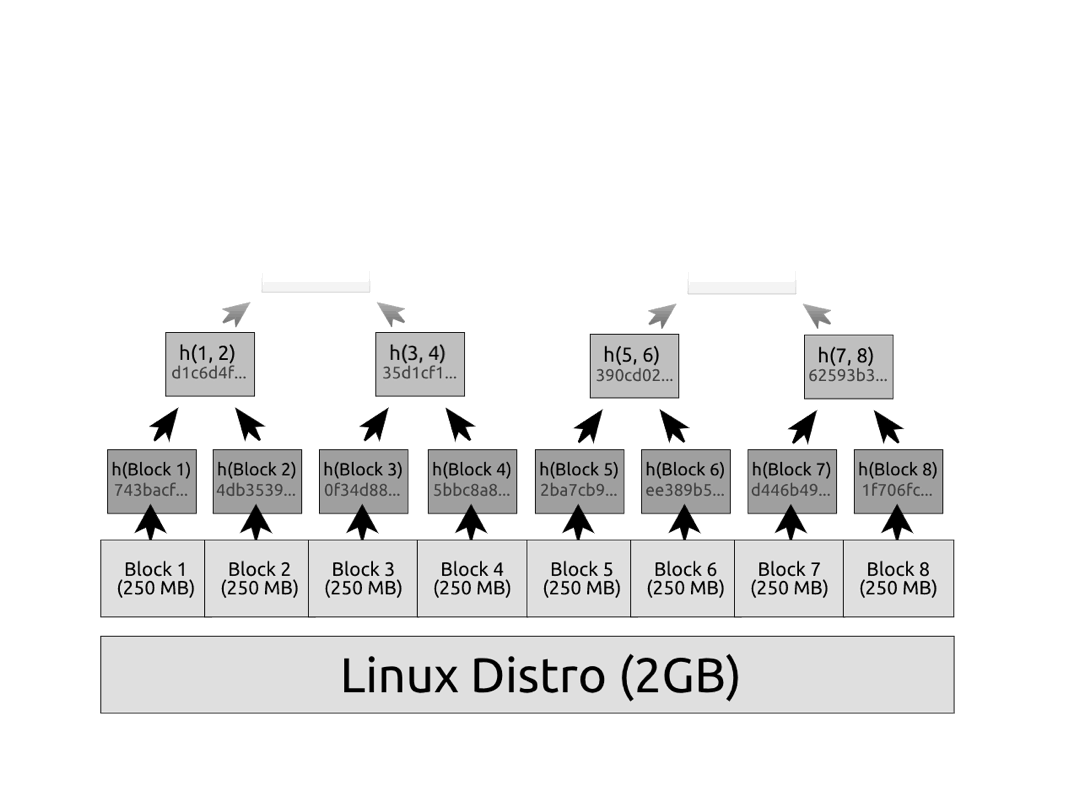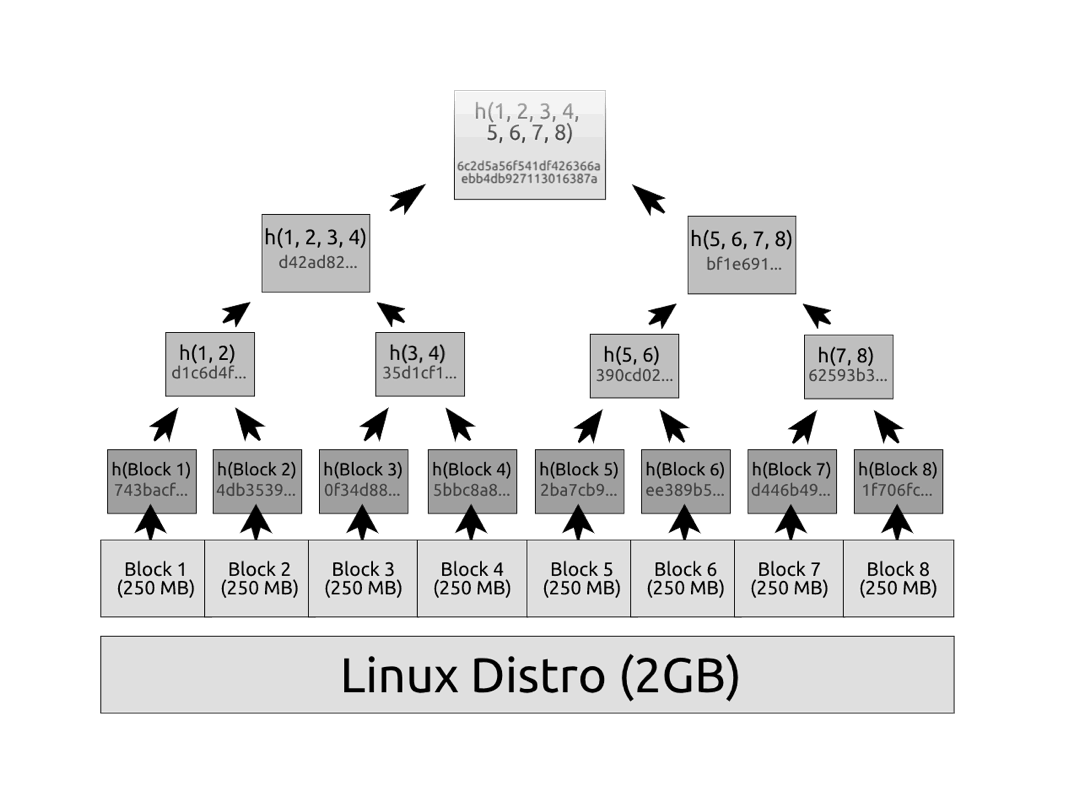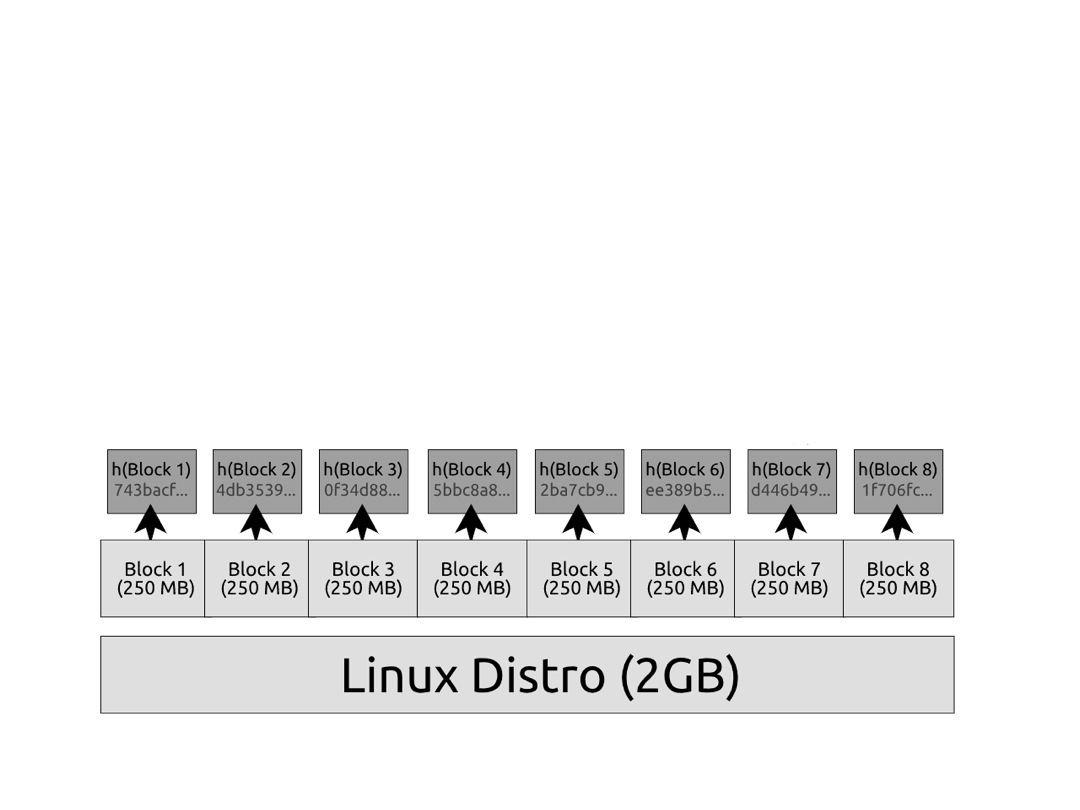
So the root of this tree is 6c2d5a56f541df426366aebb4db927113016387a. Notice that if you modified any element of the tree, even by 1 bit, then the avalanche effect of the hash would cause every hash upstream to change, all the way up to the root.

Now, say we downloaded the Linux distro along with its Merkle root (a single hash). We recompute the Merkle tree over the Linux distro on our side, and we find that our root doesn't match the one we were provided. This means our file is corrupted.
How can we quickly diagnose which of the blocks we downloaded was faulty? See if you can figure this out for yourself.
Here's the answer: we have to request the two hashes below the root in the canonical Merkle tree, and figure out which hash doesn't match up with our client-side tree. Once we've figured it out which subtree is faulty, we can repeat this for the two children of that subtree, and so on until we reach the base. Assuming there's a single faulty block, this will let you pinpoint that block with only \(O(\log{n})\) comparisons (where \(n\) is the number of underlying data blocks).
Inclusion proofs
We've seen how powerful Merkle trees are for verifying file integrity. But the real power of cryptographic accumulators comes not just in accumulating data, but in then being able to efficiently prove claims about the data.
Imagine an accumulator as an opaque box full of items. You can't directly look inside this box, but with the magic of cryptography, you can query it in specific ways.
One of the operations you can perform with a cryptographic accumulator is an inclusion proof. This is a small proof that decisively attests that an item exists in the accumulator.
If you know the Merkle root of an e-book, how can I efficiently prove to you that a certain quotation comes from that e-book? I can do this without providing you the entire e-book or even the entire Merkle tree.
Take a moment and see if you can sketch out how to do this without reading on.
Have an idea? The animation below demonstrates the answer for a simple 4-word e-book.

We only need to provide the data we're proving exists, the Merkle root, and sibling hashes along the path from the leaf up to the root. This should require only \(O(\log{n})\) hashes to transmit over the wire. If you redo all of the hashing and the roots match, you will know with certainty that quotation was indeed part of the e-book. This kind of proof is known as a Merkle proof.
You should be asking: why is this sufficient for an inclusion proof? What if someone just makes up the sibling hashes to make the roots match? How do we know they came from the real Merkle tree?
I'll leave this to you to think through for yourself.
Merkle trees in Bitcoin
Inclusion proofs are a powerful primitive enabled by Merkle trees. They are used extensively in Bitcoin light clients, also known as SPV (Simple Payment Verification) nodes. We'll do a quick sneak preview of how this works.
In Bitcoin, all the transactions that took place in the last ~10 minutes are bundled together into a block and transmitted to everyone in the network. These blocks can be quite large, since they potentially contain thousands of transactions.
To save on bandwidth, Bitcoin pulls off a clever trick: instead of transmitting all of the transactions, the transmitted block only includes a Merkle root of that block's transactions. (In practice, this transmitted data is known as a block header, while the transactions themselves are transmitted separately on request. We'll learn more about this later.)

Since a Merkle root is a cryptographic accumulator over all the underlying ordered data, every block header includes a commitments to all the transactions in that block. Because of this optimization, lightweight clients only need to keep track of block headers and can selectively verify Merkle proofs that a certain transaction was included in a given block. This optimization is essential for mobile phones or web wallets to be able to use the Bitcoin network without having to download everything.
Don't worry if that's confusing; there's a lot of structure to Bitcoin that we'll explain in upcoming lessons. But by now you have gotten a glimpse of how useful Merkle trees can be.
There are many more innovations on Merkle trees that are worth exploring, including proofs of non-inclusion, online updates, and n-ary Merkle trees. We'll provide resources in the additional reading if you want to see how the state of the art has evolved. We will also provide reading on a subtle second preimage attack against a naive implementation of a Merkle tree (though it's not of practical use in a blockchain setting).
Assignment
In our next assignment, you'll be writing your own implementation of a Merkle tree. You'll then be writing code to verify Merkle proofs.
Save your code from this, as you may find it useful for your cryptocurrency project if you choose to implement a Merkle tree.
Once you've completed the coding assignment, you're ready to move on.
Additional reading
- Second preimage attacks on Merkle trees by Dean Jerkovich (2018)
- Sparse Merkle trees, which allow efficient proofs of non-inclusion, by Faraz Haider (2018)
- Merkle Mountain Ranges by Ignotus Peverell (2018)
- Understanding Merkle pollards, which make repeated proofs more efficient, by Jim McDonald (2019)
- Merkling in Ethereum by Vitalik Buterin (2015)




